(home)

Master's Thesis: Optimization Techniques for Trustworthy 3D Object Understanding

I submitted my master's thesis to the department on Friday, May 16. It's focused on fundamental algorithms for estimating the position, orientation, and shape of objects. When available, you can download a draft here. Here's a brief outline:

1. Preliminaries. A review of the mathematics, including Shor's relaxation, conformal prediction, and quaternion algebra.

2. Certifiable Object Tracking. We propose an algorithm to track objects and estimate their shape over multiple observations. It's globally optimal in the certifiable sense. Compared to the publication, we add a world-frame motion model which is significantly faster.

3. Conformal Pose Uncertainty. Pose estimation with statistically valid translation and rotation bounds. We propagate conformal prediction bounds from the measurements (keypoints) to a pose uncertainty set, and efficiently bound the set using an ellipse.

4. Sub-Millisecond Local Pose and Shape Estimates. We rewrite the first-order optimality conditions as a nonlinear eigenproblem which can be solved in less than a millisecond using self-consistent field iteration. Solutions are local (no certificate), but can update quickly.

Extra Videos

Certifiable tracking

Conformalized pose estimates

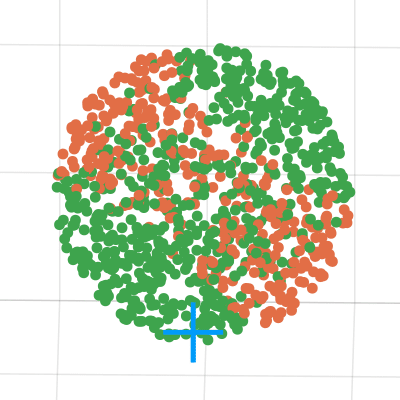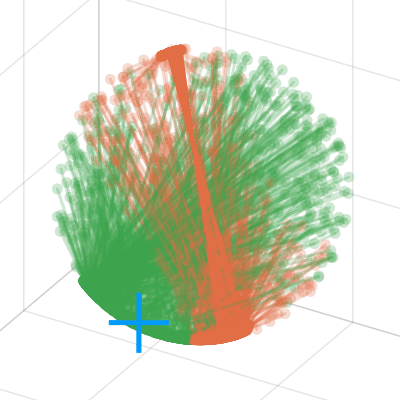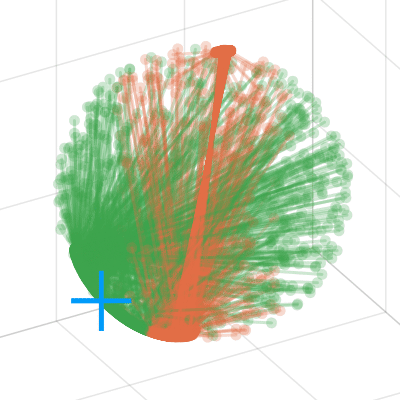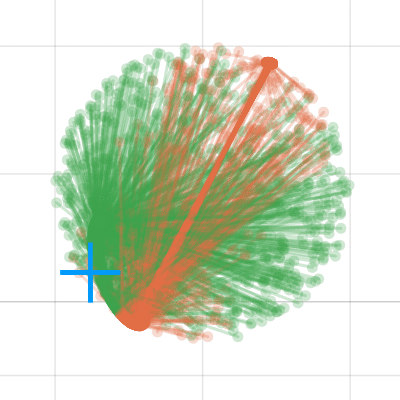
Some examples of conformal uncertainty sets (rotational uncertainty for fixed translation):

A video showing the central pose estimate for the "duck" object (if the video is broken, try a different browser or download):

Self-consistent field iterations

These animations show the trajectory of self-consistent field iteration as stereographic projections of quaternions onto the volume of the unit ball. Left, a single SCF trajectory which quickly converges. Center, an example problem where any initialization leads to the same optima. Right, an example problem where starting at an orange point leads to one minimum, and starting at a green point leads to a distinct minimum. The cross marker shows the ground truth.

Poster

BibTeX

@misc{Coming soon!}

Related Papers