Revisiting CAST: World-Frame Motion Model
Last year I published my first paper with SPARK lab, proposing a Certifiably optimal Algorithm for object Shape estimation and pose Tracking over time (CAST). The tracking problem is a fundamentally non-convex optimization problem due to the presence of rotations. Despite this, we showed that reformulating the problem as a quadratically-constrained quadratic program led to a tight convex relaxation in many real-world scenarios. It's part of a line of research that shows many NP-hard problems are often polynomial time in common robotics applications.
The post revists a key part of CAST: the constant-twist motion model for between-frame motion. I do not go into great detail on the algorithm or relaxation here; please refer to the paper.
Edit (June 2025): CAST-W has been fleshed out in my Master's thesis, also available below.
Lorenzo Shaikewitz
D-Space / video / bibTeX
Lorenzo Shaikewitz, Samuel Ubellacker, and Luca Carlone
RA-L / arXiv / code / video / bibTeX
Part 1: The Motion Model
A key idea in object tracking is to enforce physically plausable object motion across frames. We impose a motion model, which essentially enforces continuity of motion (and perhaps biases that motion from knowledge of the object dynamics). For example, car tracking algorithms often use a constant velocity and turn rate model. Even more common is just constant velocity or constant acceleration.
CAST uses a constant-twist motion model. This keeps the twist vector (body frame velocity and rotation rate) constant across frames. Visually, it models a spiral motion:
We really use a noisy version of this model: velocity \(v\) is constant up to random Gaussian noise \(\epsilon\sim\mathcal{N}(0,\Sigma)\), and rotation rate \(\Omega\) is constant up to random Langevin noise \(R_\epsilon\sim\mathcal{L}(\kappa)\). Mathematically, this is pretty simple:
\[ v_{t+1} = v_t + \epsilon_v, \quad \Omega_{t+1} = \Omega_t R_\epsilon \]The "constant-twist" part refers to updating rotations \(R\) and positions \(p\) in the body frame:
\[ p_{t+1} = p_t + R_t v_t,\quad R_{t+1} = R_t\cdot \Omega_t \]Constant World-Frame Velocity
The constant-twist motion model (2) works, and that alone is an interesting theoretical contribution to the space of certifially optimal algorithms. However, the bilinear constraints \(R_t v_t\) are inconvenient; they prevent marginalizing out position and velocity in terms of rotation and reducing the size of the optimization problem.
As we will see, the constant world-frame velocity model does not have this issue, significantly speeding up computation. At face, the world-frame velocity model seems like an excessive simpliciation. It models straight line motion of a spinning object:
There aren't a lot of objects that move this way–most are constrained to a plane (the ground) or rotate their velocity with their orientation. However, we can add noise as in (1) which essentally represents general continuous motion:
For short time frames, this should do the job of enforcing continuous motion.
Part 2: Marginalizing Postion & Velocity
The constant world-frame velocity motion model is clearly less accurate, but it allows marginalizing out position and velocity. In short, the problem is convex holding rotations constant; the first order conditions describe the optimal \(p\) and \(v\) given \(R\).
Let's work through a simpler version of the problem, omitting the shape vector and angular velocity terms. This is for ease of presentation; it does not fundamentally change the algebra.
\[ \min_{\substack{R_t\in\mathrm{SO}(3)\\s_t, v_t\in\mathbb{R}^3}} \sum_{t=1}^T \|R_t y_t - s_t\|^2 + \sum_{t=1}^{T-1} \|v_{t+1} - v_t\|^2\\ \mathrm{s.t.\:} s_{t+1} = s_t + v_t,\:t=1,...,T-1 \]The constant world-frame velocity model is the constraint \(s_{t+1} = s_t + v_t\). Crucially, the position \(s_t\) is only a function of \(v\), not any rotations. This optimization problem is convex in \(v_t\) and \(s_t\) holding \(R_t\) constant, so we can solve it via first-order conditions. The Lagrangian is:
\[ L(s, v, \lambda) = \sum_{t=1}^T \|R_t y_t - s_t\|^2 + \sum_{t=1}^{T-1} \|v_{t+1} - v_t\|^2 + \lambda_t(s_{t+1}-s_t-v_t) \]Taking the derivative, we have the following equations:
\[ 0=\nabla_{s_t}L = 2s_t - 2R_ty_t + (\lambda_{t-1} - \lambda_t) \] \[ 0 = \nabla_{v_t}L = 4v_t - 2v_{t+1} - 2v_{t-1} - \lambda_t \]Together with the equality constraint \(s_{t+1} = s_t + v_t\), we have a linear system of equations:
\[ A \begin{bmatrix} s \\ v \\ \lambda \end{bmatrix} = b(R) \]where \(A\) is composed of the (constant) coefficients of \(s,v,\lambda\) in the first order conditions and equality constraint, while \(b\) is the terms which do not depend on \(s,v,\lambda\). In particular, \(A\) is independent of \(R\) and \(b(R)\) is a linear function of \(R\). Thus, inverting \(A\) allows solving for \(s\) and \(v\) in closed form in terms of \(R\). Plugging this in to the objective does not change the QCQP form. It only reduces the decision space, significantly speeding up computation.
Part 3: Speed
The major advantage of the world-frame velocity model is pure speed. Empirically, it runs around 5 times faster than the body-frame velocity model, depending on the number of times steps \(T\) we consider. For short time steps, the performance of the more realistic body-frame velocity model is almost indistinguishable from the world-frame velocity model. I show this on the real-world drone tracking data from our paper:
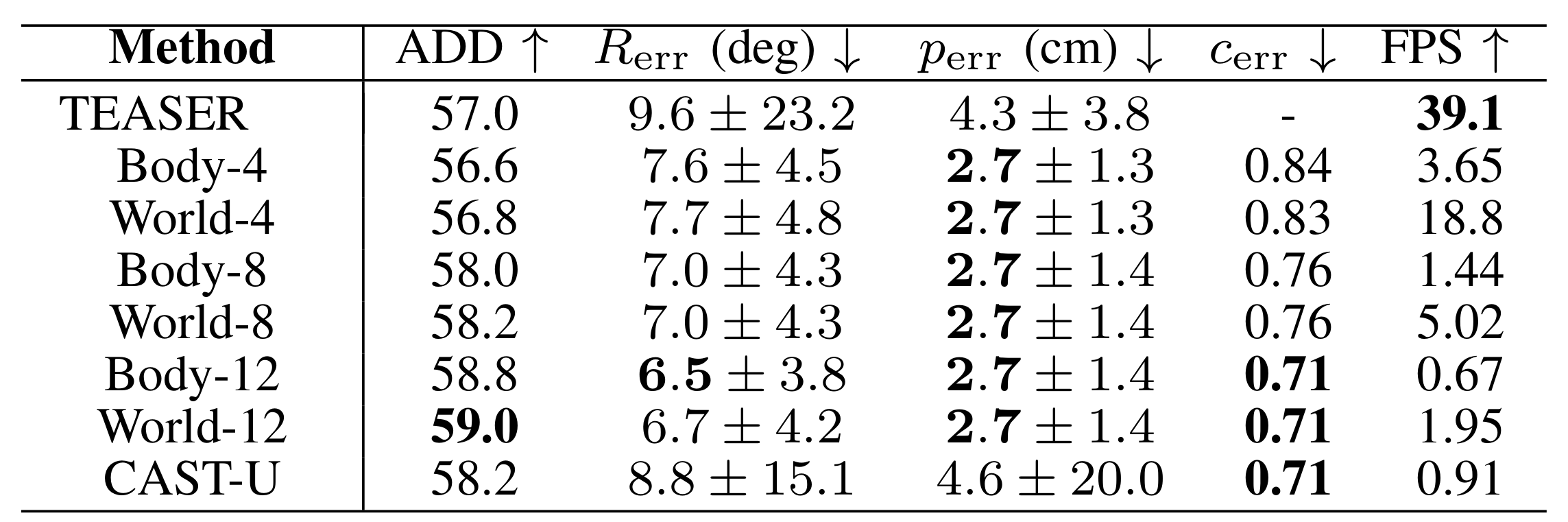
It seems like we can have our cake and eat it too: we can use a simpler model and marginalize position and velocity for significant speed improvements without sacrificing accuracy. As long as we run tracking fast enough, any first-order approximation will be reasonable and the fixed-lag will take care of large, long-term deviations from the motion model.
I don't want to completely dismiss the body-frame model. A unique part of working with convex relaxations is the art of making an informed guess about whether a relaxation is tight. From that perspective, a body-frame model is interesting because it remains tight despite the bilinear motion model. Further, we expect the body-frame model to be much more accurate as the time step between samples grows.
I want to thank Prof. Zac Manchester for suggesting we take a closer look at the world-frame model.
Code for Visuals
Constant-Twist (Body-Frame Velocity) Motion
# spiral
t = LinRange(0,6*π,1000)
Plots.plot3d(cos.(t), sin.(t), t,label="trajectory")
t2 = LinRange(0.5,5*π+2, 8)
Plots.scatter3d!(cos.(t2), sin.(t2), t2,label="samples")
Plots.quiver!(cos.(t2),sin.(t2),t2, quiver=(-0.5*sin.(t2), 0.5*cos.(t2), 0.5*ones(8)), color=:red)
Plots.quiver!(cos.(t2),sin.(t2),t2, quiver=(0.5*cos.(t2), 0.5*sin.(t2), -0.5*zeros(8)), color=:green)
# Plots.quiver!(cos.(t2),sin.(t2),t2, quiver=(-0.5*sin.(t2), 0.5*cos.(t2), -0.5*ones(8)), color=:blue)World-Frame Velocity Motion
# straight line
t = LinRange(0,6*π,1000)
Plots.plot3d(0 .*t, 0 .*t, t, label="trajectory", ylim=[-0.5,0.5], xlim=[-0.5,0.5])
t2 = LinRange(0.5,5*π+2, 8)
Plots.scatter3d!(0 .*t2, 0 .*t2, t2,label="samples")
scale = 0.15
Plots.quiver!(0*t,0*t,t2, quiver=(-scale*sin.(t2), scale*ones(8), scale*cos.(t2)), color=:red)
Plots.quiver!(0*t,0*t,t2, quiver=( scale*cos.(t2), -scale*zeros(8), scale*sin.(t2)), color=:green)
# Plots.quiver!(0*t,0*t,t2, quiver=(scale*sin.(t2), scale*ones(8), -scale*cos.(t2)), color=:blue)